Растяжение и сжатие графиков функций

Список функций, изученных в 7 и 8 классе

Функция	Формула	График	Раздел справочника
Прямая пропорциональность	y = kx	Прямая	7 кл., §37
Линейная функция	y = kx+b	Прямая	7 кл., §38-39
Обратная пропорциональность	$ y = frac{k}{x} $	Гипербола	8 кл., §6
Квадрат числа	$ y=x^2$	Парабола	8 кл., §18
Квадратный трёхчлен	$ y = ax^2+bc+c$	Парабола	8 кл., §28-29
Квадратный корень	$ y = sqrt{x}$	Парабола	8 кл., §22

Растяжение и сжатие графика по оси OX

Сравним графики пар функций, которые в общем виде можно записать так:

$$ y_1 = f(x), y_2 = f(px) $$

где $p gt 1$, произвольный положительный множитель.

Пусть p = 2.

Парабола: $y_1 = f(x) = x^2$ $ y_2 = f(2x) = (2x)^2 = 4x^2 $ $y_2 = y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f(2x) = frac{4}{(2x)} = frac{2}{x}$ $ y_2 = y_1 при x_2 = frac{1}{2} x_1 $ График сжимается в 2 раза по оси OX
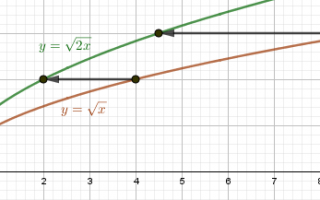
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f(2x) = sqrt{2x}$ $y_2=y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX

Теперь сравним пары функций с делением на p:

$$ y_1 = f(x), quad y_2 = f left( frac{x}{p} right), quad p gt 1 $$

Пусть p = 2

Парабола: $y_1 = f(x) = x^2$ $ y_2 = f left(frac{x}{2}right) = left(frac{x}{2}right)^2 = frac{x^2}{4} $ $y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f left(frac{x}{2}right) = frac{4}{x/2} = frac{8}{x}$ $ y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f left(frac{x}{2}right) = sqrt{frac{x}{2}}$ $y_2=y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX

При сравнении графиков двух функций

$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$

график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.

При сравнении графиков двух функций

$$ y_1 = f(x), quad y_2 = f Biggl(frac{x}{p}Biggr), quad p gt 1 $$

график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.

Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)

Растяжение и сжатие графика по оси OY

Сравним графики пар функций, которые в общем виде можно записать так:

$$ y_1 = f(x), quad y_2 = Af(x) $$

где $A gt 1$, произвольный положительный множитель.

Пусть A = 2.

Парабола: $y_1 = f(x) = x^2$ $ y_2 = 2f(x) = 2x^2 $ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = 2f(x) = frac{8}{x}$ $ y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = 2f(x) = 2sqrt{x}$ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY

Теперь сравним пары функций с делением на A:

$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$

Пусть A = 2

Парабола: $y_1 = f(x) = x^2$ $ y_2 = frac{1}{2}f(x) = frac{x^2}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = frac{1}{2}f(x) = frac{2}{x}$ $ y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = frac{1}{2}f(x) = frac{sqrt{x}}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY

При сравнении графиков двух функций

$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$

график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.

При сравнении графиков двух функций

$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$

график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.

Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)

Примеры

Пример 1. Постройте в одной координатной плоскости графики функций:

$$ y = sqrt{x}, y = sqrt{3x}, y = sqrt{frac{x}{3}}, y = 3sqrt{x} $$

Сделайте выводы.

По сравнению с графиком $y = sqrt{x}$:

• график функции $y = sqrt{3x}$ сжимается в 3 раза по оси OX(←)
• график функции $y = sqrt{frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
• график функции $y = 3sqrt{x}$ растягивается в 3 раза по оси OY(↑)

Пример 2*. Постройте в одной координатной плоскости графики функций:

$$ y = f(x), y = f(2x), y = f Biggl(frac{x}{2}Biggr), y = 2f(x) $$

где $f(x) = x^2+3x+2$

Сделайте выводы.

Исходная функция $y = f(x) = x^2+3x+2$

Остальные функции

$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$

$$ y = fBiggl(frac{x}{2}Biggr) = Biggl(frac{x}{2}Biggr)^2+3 cdot Biggl(frac{x}{2}Biggr) +2 = frac{x^2}{4}+ frac{3}{2} x+2 $$

$$ y = 2f(x) = 2x^2+6x+4 $$

Получаем:

По сравнению с графиком $y = f(x) = x^2+3x+2$:

• график функции y = f(2x) сжимается в 2 раза по оси OX(→)
• график функции $y = f left(frac{x}{2}right)$ растягивается в 2 раза по оси OX(←)
• график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)

Рейтинг пользователей

Конспект урока + презентация по теме «Преобразование графиков функций»

Предмет:	Математика
Тема урока по учебно-тематическому плану:	Урок по теме «Преобразование графиков функций»
Форма урока:	Урок формирования новых знаний
Цель:	Научить обучающихся строить графики сложных функций с использованием параллельного переноса, растяжения, сжатия, симметрии относительно осей координат графиков известных функций, показать построение графиков, содержащих модуль, а также с последовательным применением нескольких способов.
Задачи:	Образовательные: Вспомнить основные числовые и тригонометрические функции, их графики; рассмотреть геометрические преобразования графиков функций и научить строить графики сложных функций Развивающие: Развивать у обучающихся умение логически мыслить, классифицировать, обобщать, анализировать математические ситуации Воспитательные: Воспитывать познавательную активность, самостоятельность, упорство в достижении цели. Побуждать обучающихся к самоконтролю, взаимоконтролю, самоанализу своей деятельности
Оборудование, учебные материалы:	Мультимедийный проектор, компьютер, опорные конспекты, учебник
Методы обучения:	Словесный, практический, наглядный, вопросно-ответный
Формы педагогической деятельности	Активизация знаний и внимания, беседа, создание учебных познавательных и коммуникативных ситуаций
Формы организации познавательной деятельности	Индивидуальная, фронтальная, групповая
Ожидаемые результаты:	Обучающиеся должны знать основные функции, уметь определять вид их графика, строить графики, уметь строить графики сложных функций, используя метод преобразования

Этапы урока

Во фронтальной беседе с обучающимися повторяются необходимые для

изучения данной темы знания ребят.

Перечисляют знакомые по курсу алгебры функции, их графики, отгадывают кроссворд.

3

Изучение нового материала.

Объяснение нового материала.

Заполняют опорные конспекты, отвечают на вопросы преподавателя

4

Закрепление изученного материала.

Объяснение заданий.

Обсуждают построение графиков вместе с преподавателем, строят графики в тетради, а затем сверяют с графиками на экране.

Отвечают на вопросы учителя.

Выполняют устный тест.

5

Самостоятельная работа по новому материалу.

Проверка выполнения задания

Выполняют задания.

6

Подведение итогов.

Подведение итогов урока.

7

Задание на дом.

Объяснение домашнего задания.

Записывают задание на дом.

Ход урока

1. Организационный этап.

Обучающиеся отгадывают шуточную загадку (слайд 1). После этого преподаватель объявляет, что героем урока является, его величество, график.

Объявление целей урока (слайды 2-3)

Н.Е.Жуковский сказал: «В математике есть своя красота, как в живописи и поэзии». Сегодня на уроке мы научимся очень красивому методу построения графиков функции — методу преобразований.

2. Повторение. Фронтальный опрос.

Вопросы:

1. Определение графика функции (слайд 5)

2. Отгадать кроссворд (слайд 6-11)

3. Какие функции вам знакомы из курса алгебры 7-9 классов? Давайте вспомним, как выглядят графики этих функций?

3. Объяснение нового материала.

Учитель показывает на примерах построение графиков у = f (x+a), y = f (x) + b, y = — f (x), y = f (-x), y = kf (x)… с использованием графика функции у = f (х) (слайды 12-28). Во время объяснения учащиеся заполняют листы опорных конспектов (строят полученные в ходе преобразования графики)

4. Закрепление нового материала.

• Построение графиков функций.

• Вместе с преподавателем учащиеся анализируют способ построения графиков, после строят в тетради самостоятельно и сверяют с графиками на экране (слайды 29-33).

• Определение вида преобразований, определение формулы функции (слайды 34, 35).

• Выполнение теста. Найдите соответствующие графики функций (слайды 36-39).

5. Самостоятельная работа (индивидуальный тренинг) (слайд 40).

Критерии оценок:

• 5-7 баллов — «3»

• 8-10 баллов — «4»

• 11-12 баллов — «5»

Дополнительные задания решаются на дополнительную оценку.

6. Подведение итогов урока.

Графики функции широко используются в различных областях науки, поэтому умение строить, «читать», прогнозировать их «поведение», имеет огромную роль в практической деятельности в инженерной области, гидрометеорологов и людей других математических специальностей.

7. Задание на дом (Слайд 41)

№ 49 (в, г); 50 (в, г);

* № 55 (a, б); 56 (а, б).

Творческое задание: придумать графики функций, с помощью которых можно нарисовать рисунок.

Конспект по теме «Преобразование графиков функций»

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x) + a, где а — постоянное число, надо перенести график функции f(x) на а единиц вверх вдоль оси оу.

Для построения графика функции y = f (x) — a, где а — постоянное число, надо перенести график функции f(x) на а единиц вниз вдоль оси оу.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x) + a, где а — постоянное число, надо перенести график функции f(x) на а единиц вверх вдоль оси оу.

Для построения графика функции y = f (x) — a, где а — постоянное число, надо перенести график функции f(x) на а единиц вниз вдоль оси оу.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x) + a, где а — постоянное число, надо перенести график функции f(x) на а единиц вверх вдоль оси оу.

Для построения графика функции y = f (x) — a, где а — постоянное число, надо перенести график функции f(x) на а единиц вниз вдоль оси оу.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x) + a, где а — постоянное число, надо перенести график функции f(x) на а единиц вверх вдоль оси оу.

Для построения графика функции y = f (x) — a, где а — постоянное число, надо перенести график функции f(x) на а единиц вниз вдоль оси оу.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x-а) , где а — постоянное число, надо перенести график функции f(x) вдоль оси ох вправо на а единиц .

Для построения графика функции y = f (x+а), где а — постоянное число, надо перенести график функции f(x) вдоль оси ох влево на а единиц.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x-а) , где а — постоянное число, надо перенести график функции f(x) вдоль оси ох вправо на а единиц .

Для построения графика функции y = f (x+а), где а — постоянное число, надо перенести график функции f(x) вдоль оси ох влево на а единиц.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x-а) , где а — постоянное число, надо перенести график функции f(x) вдоль оси ох вправо на а единиц .

Для построения графика функции y = f (x+а), где а — постоянное число, надо перенести график функции f(x) вдоль оси ох влево на а единиц

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y = f (x-а) , где а — постоянное число, надо перенести график функции f(x) вдоль оси ох вправо на а единиц .

Для построения графика функции y = f (x+а), где а — постоянное число, надо перенести график функции f(x) вдоль оси ох влево на а единиц.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y =K f (x) , где k — постоянное число, надо растянуть график функции f(x) в K раз вдоль оси оу.

Для построения графика функции y =f (x) , где k — постоянное число, надо сжать график функции f(x) в K раз вдоль оси оу.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y =K f (x) , где k — постоянное число, надо растянуть график функции f(x) в K раз вдоль оси оу.

Для построения графика функции y =f (x) , где k — постоянное число, надо сжать график функции f(x) в K раз вдоль оси оу.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y =K f (x) , где k — постоянное число, надо растянуть график функции f(x) в K раз вдоль оси оу.

Для построения графика функции y =f (x) , где k — постоянное число, надо сжать график функции f(x) в K раз вдоль оси оу.

ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Для построения графика функции y =K f (x) , где k — постоянное число, надо растянуть график функции f(x) в K раз вдоль оси оу.

Для построения графика функции y =f (x) , где k — постоянное число, надо сжать график функции f(x) в K раз вдоль оси оу.

Урок по теме «Преобразования графиков»

27.09.2020 г.

План-конспект урока

по теме «Преобразования графиков»

(урок алгебры, 10 «4» класс, 2 ч.)

Урок — лекция

Цели: повторить, закрепить и обобщить понятие функции, графика функции; рассмотреть геометрические преобразования графиков функций, выработать у учащихся навыки по построению графиков функций, используя различные их преобразования; развивать логику, мышление.

Ход урока:

I. Организационный момент

II. Проверка домашнего задания

III. Устная работа

1. №44 (в), №51(б)

2. Привести пример аналитически заданной функции, определенной:

а) на всей числовой прямой; (f(x) =х2 + 2х — 3)

б) на всей числовой прямой, кроме точки х = 2; (f(x) = )

в) на всей числовой прямой, кроме точек х = — 1; 1;

(f(x) = )

г) на [0; + ∞); (f(x) = )

д) на [- 2; 2]. (f(x) = )

IV. Работа по учебнику (с помощью рисунков)

1. Проверить решение №46 (устно по рис.27)

2. Устно решить №42 (по рис.26)

3. Решить на доске №47.

IV. Изучение нового материала (лекция)

Запас функций, графики которых вы умеете строить, пока невелик — это функции y = kx + b, y = ax2 + bx + c, y = , y = sin x, y = cos x, y = tg x, y = ctg x. Покажем, что, применяя известные из курса геометрии сведения о преобразованиях фигур, этот список можно существенно расширить.

1) Рассмотрим сначала параллельный перенос на вектор (0; b) вдоль оси ординат. Обозначая здесь и далее через (х/; y/) координаты точки, в которую переходит произвольная точка (х; у) плоскости при данном преобразовании, получим известные вам формулы

(1)

Пусть f — произвольная функция с областью определения D(f). Выясним, в какую фигуру переходит график этой функции при данном переносе. Из формул (1) сразу получаем, что произвольная точка (x; f(x)) графика переходит в точку (x; f(x) + b). Это означает, что график f переходит в фигуру, состоящую из всех точек (x; f(x) + b), где х € D(f).

По определению графика функции эта фигура является графиком функции у = f(x) + b. Сказанное позволяет сформулировать правило:

Для построения графика функции f(x) + b, где b — постоянное число, надо перенести график f на вектор (0; b) вдоль оси ординат.

Пример 1

Построим графики функций: а) y = sin x + 2.

y

y = sin x + 2

у = sin x 1

— 3 π — 2 π — π 0 π 2 π 3 π х

— 1

В соответствии с правилом переносим график функции y = sin x на вектор (0; 2), т. е. вверх по оси Оу на 2 единицы.

б) y = x2 — 5.

y

y = x2

y = x2 — 5

-1 0 1 x

— 5

Построение осуществляется переносом параболы y = x2 на вектор (0; -5), т. е. вниз по оси Оу на 5 единиц.

2) Новым для вас преобразованием является растяжение вдоль оси Оу с коэффициентом k, которое задается формулами

(2)

Для построения точки М/, в которую переходит данная точка М при растяжении, надо построить на прямой АМ, где А — проекция М на ось Ох, точку, гомотетичную М относительно центра А (коэффициент гомотетии равен коэффициенту k растяжения).

Выясним, в какую фигуру переходит график функции f при растяжении. Из формул (2) сразу получаем, что произвольная точка (x; f(x)) графика f переходит в точку (x; k f(x)). Отсюда следует, что график f переходит в фигуру, состоящую из всех точек (x; k f(x)), где x € D(f). Эта фигура является графиком функции у = k f(x).

Сказанное позволяет сформулировать правило:

Для построения графика функции у = k f(x) надо растянуть график функции у = f(x) в k раз вдоль оси ординат.

Пример 2

Построим графики функций: а) y = — 2×2; б) y = cos x.

у

у = 2х2

у = х2

2 М/

-2 -1 0 1 2 х

-2 M//

у = — 2х2

б) y = cos x.

у

1 у = cos x

y = 1/3 cos x

— π — π/2 0 π/2 π х

-1

Построение осуществляется в первом случае из графика функции у = х2, а во втором случае сначала строим график функции у = cos x, а затем воспользуемся растяжением вдоль оси ординат с коэффициентом .

Замечание. Если 0 < | k | < 1, то растяжение с коэффициентом k часто называют сжатием. Например, растяжение с коэффициентом называют сжатием в 2 раза. Отметим также, что если k < 0, то для построения графика функции y = k f(x) надо сначала растянуть график f в | k | раз, а затем отразить его симметрично относительно оси абсцисс.

3) Параллельный перенос вдоль оси абсцисс на вектор (а; 0) задается формулами

(3)

Каждая точка графика функции f переходит согласно формулам (3) в точку (х + а; f(x)). Поэтому с помощью переменных x/, y/ можно записать, что график f переходит в фигуру Ф, состоящую из точек (x/; f(x/ — a)), где x/ принимает все значения вида х + а (x «пробегает» D(f)).

Именно при этих значениях x/ число x/ — а принадлежит D(f) и f(x/ — а) определено. Следовательно, фигура Ф есть график функции y = f(x — a). Итак, можно сделать вывод:

График функции y = f(x — a) получается из графика f переносом (вдоль оси абсцисс) на вектор (а; 0).

Обратите внимание: если а > 0, то вектор (а; 0) направлен в положительном направлении оси абсцисс, а при а < 0 — в отрицательном.

Пример 3

Построение графиков функций y = и y = cos (x — ).

у у = у =

M/ M

— 1 0 1 х

у

1 y = cos(x — π/4) у = cos x

M M/

— π 0 π х

-1

4) Растяжение вдоль оси Ох с коэффициентом k задается формулами

(4)

Произвольная точка графика функции f переходит при таком растяжении в точку (kx; f(x)). Переходя к переменным x/, y/, можно записать, что график y = f(x) переходит в фигуру, состоящую из точек (x/; f()), где x/ принимает все значения вида x/ = kx, а x € D(f).

Эта фигура есть график функции y = f(). Итак:

Для построения графика функции y = f() надо подвергнуть график функции f растяжению с коэффициентом k вдоль оси абсцисс.

Пример 4

Построение графиков функций y = cos 2x и y = sin x.

у

1 у = cos 2x

— π 0 π х

-1 y = cos x

y

y = sin x

1

— π 0 π x

— 1 y = sin x

V. Закрепление изученного материала.

1. Повторить виды преобразований.

2. № 56 (устно).

VI. Итоги урока.

VII. Домашнее задание.

§2, п. 3 (выучить), № 54, №55.

Литература:

1. М.П. Киселева, З.С. Шпрах, Л.М. Борисова и др. Доклиническое изучение противоопухолевой активности производного N-гликозида индолокарбазола ЛХС-1208. Сообщение I // Российский биотерапевтический журнал. 2015. № 2. С. 71-77.
2. Мустафин Р. И., Протасова А. А., Буховец А. В., Семина И.И. Исследование интерполимерных сочетаний на основе (мет)акрилатов в качестве перспективных носителей в поликомплексных системах для гастроретентивной доставки. Фармация. 2014; 5: 3–5.
3. https://reshator.com/sprav/algebra/8-klass/rastyazhenie-i-szhatie-grafikov-funkcij/.
4. https://infourok.ru/konspekt-uroka-prezentaciya-po-teme-preobrazovanie-grafikov-funkciy-1690965.html.
5. https://infourok.ru/konspekt-po-teme-preobrazovanie-grafikov-funkciy-2399655.html.
6. https://infourok.ru/urok-po-teme-preobrazovaniya-grafikov-5005614.html.
7. З.С. Смирнова, Л.М. Борисова, М.П. Киселева и др. Противоопухолевая эффективность прототипа лекарственной формы соединения ЛХС-1208 для внутривенного введения // Российский биотерапевтический журнал. 2012. № 2. С. 49.
8. А.В. Ланцова, Е.В. Санарова, Н.А. Оборотова и др. Разработка технологии получения инъекционной лекарственной формы на основе отечественной субстанции производной индолокарбазола ЛХС-1208 // Российский биотерапевтический журнал. 2014. Т. 13. № 3. С. 25-32.
9. Мирский, «Хирургия от древности до современности. Очерки истории.» (Москва, Наука, 2000, 798 с.).